Topological data analysis enables deep quantification of vascular responses to drug and radiation treatment in 3D tumours. Oxford Mathematician Bernadette Stolz explains.
Many complex systems, such as cities, social media, animal social groups, or brains can be represented using the framework of network science, i.e., as a set of individual units linked together through certain types of interactions.
Quantum field theory (QFT) is a natural language for describing quantum physics that obeys special relativity. A modern perspective on QFT is provided by the renormalization group (RG) flow, which is a path defined on the coupling constant space and evolves from the ultraviolet (UV) to the infrared (IR) fixed point. In particular, the theories on the IR fixed point are scale-invariant and most of them are known to be promoted to a conformal field theory (CFT).
The study of finitely generated groups usually proceeds in two steps. Firstly, a class of spaces with some intrinsic geometric property is defined and understood, for example hyperbolic spaces or CAT(0) spaces. Secondly, we try to relate the geometry of the space to algebraic properties of groups acting properly discontinuously cocompactly (i.e. geometrically) on the space. For example, this gives rise to the well studied classes of hyperbolic groups and CAT(0) groups.
The virus causing the COVID-19 pandemic, SARS-CoV-2, is transmitted through virus-carrying respiratory droplets, which are released when an infected person coughs, sneezes, talks or breathes. Most of these droplets will fall to the ground within two metres, hence the guidelines to maintain social distancing. However, some droplets are small enough to float in the air. These droplets may remain airborne for hours and be carried throughout a room, leading to airborne transmission.
The British computer scientist Christopher Strachey (1916–1975) is frequently cited as having called for an end to an “artificial and injurious” separation of practical and theoretical work in programming.
The first months of 2020 brought the world to an almost complete standstill due to the occurrence and outbreak of the SARS-CoV-2 coronavirus, which causes the highly contagious COVID-19 disease. Despite the hopes that rapidly developing medical sciences would quickly find an effective remedy, the last two years have made it quite clear that, despite vaccines, this is not very likely.
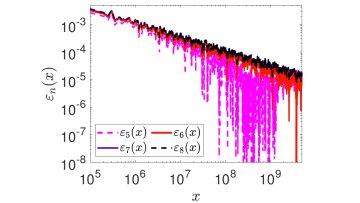
Much of theoretical physics is built on the concept of perturbation theory. Essentially perturbation theory is the idea that we can find a small quantity in the physical system we wish to describe and use that to expand the equations describing the system. In this way we obtain a simpler set of equations to solve.
Define the prime-counting function $\pi(x)$ to be the number of natural primes less than or equal to $x$.
If you have ever watched the movie Transformers you may not have worried too much about whether it is realistic. Nevertheless, scientists have tried, and are still trying, to create objects that can transform their shape.
The Riemann zeta-function is defined by \[ \zeta(s) = \sum_{n=1}^\infty \frac{1}{n^s}, \quad \text{for $\mathrm{Re}(s) > 1$}, \] and the domain is extended to all of $\mathbb{C}$ by analytic continuation. The zeros of the Riemann zeta-function are the subject of the Riemann hypothesis.
Industrial inkjets use inkjet technology - familiar to any office printer - to print or deposit materials as part of the manufacturing process of a product on a production line. It requires precise control of the formation and jetting of small droplets of liquid ink.
Curvature is a way of measuring the distortion of a space from being flat, and it is ubiquitous in Science. Ricci Curvature, in particular, appears in Einstein’s equations of General Relativity. It controls the heat diffusion in general ambient spaces and it plays a fundamental role in Hamilton-Perelman’s solution of the Poincaré conjecture and of Thurston’s geometrisation conjecture.
Today, two Oxford mathematicians András Juhász and Marc Lackenby published a paper in Nature in collaboration with authors from DeepMind and with Geordie Williamson at the University of Sydney.
Silicon is produced industrially in a submerged arc furnace (illustrated in Figure 1, left), with the heat required for the endothermic chemical reaction provided by an electric current. The high temperatures within the furnace (up to around 2000 K) prohibit observation of the internal conditions, so that mathematical modelling is a valuable tool to understand the furnace processes.
The 7m length by 2m diameter cylindrical Søderberg electrode is the secret behind a yearly production capacity of 215,000 tonnes of silicon for Elkem ASA, the third largest silicon producer in the world. This electrode operates continuously thanks to its raw material: carbon paste, whose viscosity depends very sensitively on the temperature.
A collaboration between pure and applied mathematicians, pathologists and clinicians, has shown how sophisticated techniques from computational algebraic topology can be applied to understand the spatial distributions of immune cell subtypes in the tumour microenvironment.
Alois Alzheimer called Alzheimer's disease (AD) the disease of forgetfulness in a 1906 lecture that would later mark its discovery. Alzheimer noticed the presence of aggregated protein plaques, made up of misfolded variants of amyloid-beta (A$\beta$) and tau ($\tau$P) proteins, in the brain of one of his patients. These plaques are thought to be the drivers of the overall cognitive decline that is observed in AD. AD is now one of the leading causes of death in many developed countries, including the United Kingdom.